代码随想录day32｜122.买卖股票的最佳时机II｜55. 跳跃游戏｜45.跳跃游戏II｜Golang

代码随想录day32

目录

代码随想录day32

122.买卖股票的最佳时机II

55. 跳跃游戏

45.跳跃游戏II

---

122.买卖股票的最佳时机II

本题首先要清楚两点：

• 只有一只股票！
• 当前只有买股票或者卖股票的操作

想获得利润至少要两天为一个交易单元。

贪心算法

        这道题目可能我们只会想，选一个低的买入，在选个高的卖，在选一个低的买入.....循环反复。

        如果想到其实最终利润是可以分解的，那么本题就很容易了！如何分解呢？

        假如第0天买入，第3天卖出，那么利润为：prices[3] - prices[0]。

        相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。

此时就是把利润分解为每天为单位的维度，而不是从0天到第3天整体去考虑！

        那么根据prices可以得到每天的利润序列：(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。

如图：

        一些同学陷入：第一天怎么就没有利润呢，第一天到底算不算的困惑中。第一天当然没有利润，至少要第二天才会有利润，所以利润的序列比股票序列少一天！

        从图中可以发现，其实我们需要收集每天的正利润就可以，收集正利润的区间，就是股票买卖的区间，而我们只需要关注最终利润，不需要记录区间。

那么只收集正利润就是贪心所贪的地方！

        局部最优：收集每天的正利润，全局最优：求得最大利润。

        局部最优可以推出全局最优，找不出反例，试一试贪心！

对应Go代码如下：

func maxProfit(prices []int) int {
    result := 0
    for i:=1;i<len(prices);i++{
        result += max(prices[i] - prices[i-1], 0)    //只统计每日正利润
    }
    return result
}
func max(a , b int) int {
    if a > b {
        return a
    } 
    return b
}
时间复杂度：O(n)
空间复杂度：O(1)

本题小结

        股票问题其实是一个系列的，属于动态规划的范畴，因为目前在讲解贪心系列，所以股票问题会在之后的动态规划系列中详细讲解。

        可以看出有时候，贪心往往比动态规划更巧妙，更好用，所以别小看了贪心算法。

        本题中理解利润拆分是关键点！ 不要整块的去看，而是把整体利润拆为每天的利润。

        一旦想到这里了，很自然就会想到贪心了，即：只收集每天的正利润，最后稳稳的就是最大利润了。

55. 跳跃游戏

思路

        刚看到本题一开始可能想：当前位置元素如果是3，我究竟是跳一步呢，还是两步呢，还是三步呢，究竟跳几步才是最优呢？

        其实跳几步无所谓，关键在于可跳的覆盖范围！

        不一定非要明确一次究竟跳几步，每次取最大的跳跃步数，这个就是可以跳跃的覆盖范围。

        这个范围内，别管是怎么跳的，反正一定可以跳过来。那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！

        每次移动取最大跳跃步数（得到最大的覆盖范围），每移动一个单位，就更新最大覆盖范围。

        贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。

        局部最优推出全局最优，找不出反例，试试贪心！

如图：

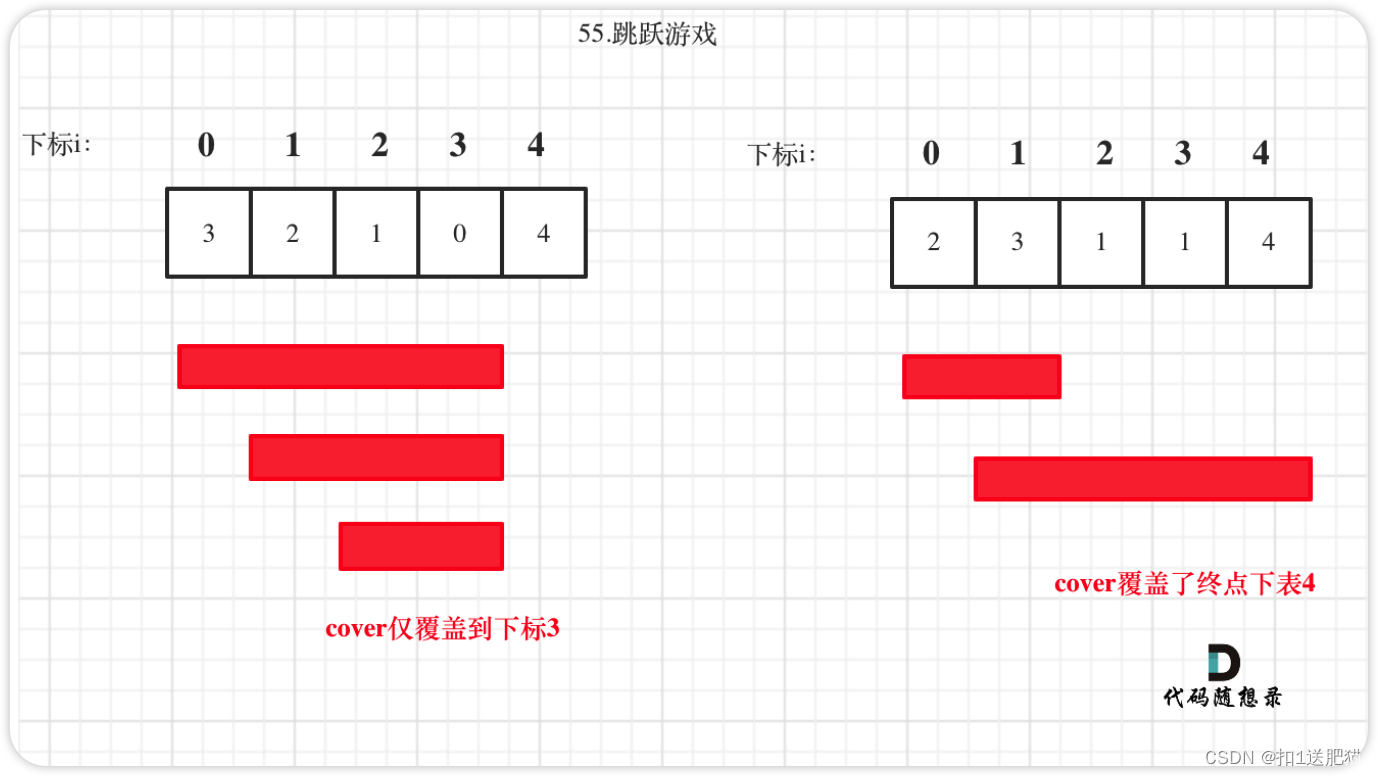
        i每次移动只能在cover的范围内移动，每移动一个元素，cover得到该元素数值（新的覆盖范围）的补充，让i继续移动下去。

        而cover每次只取 max(该元素数值补充后的范围, cover本身范围)。如果cover大于等于了终点下标，直接return true就可以了。

Go代码如下：

func canJump(nums []int) bool {
    cover := 0  // 覆盖范围
    if len(nums) == 1 {
        return true //只有一个元素的话就既是开头也是结尾。就到达了啊
    }
    for i:=0;i<=cover;i++{    //注意是小于等于cover哦
        cover = max(i+nums[i], cover)   // 更新cover，取前面的覆盖范围和当前nums[i]+i的最大作为新的覆盖范围,为什么要加i因为你不加你的没前面的长度了
        if cover >= len(nums)-1 {    //说明可以覆盖到终点了，直接true
            return true        
        }
    }
    return false
}
 
func max(a, b int) int {
    if a > b {
        return a 
    }
    return b
}

本题小结

        这道题目关键点在于：不用拘泥于每次究竟跳跳几步，而是看覆盖范围，覆盖范围内一定是可以跳过来的，不用管是怎么跳的。

        大家可以看出思路想出来了，代码还是非常简单的。一些同学可能感觉，我在讲贪心系列的时候，题目和题目之间貌似没有什么联系？

        是真的就是没什么联系，因为贪心无套路！没有个整体的贪心框架解决一些列问题，只能是接触各种类型的题目锻炼自己的贪心思维！

45.跳跃游戏II

思路

        本题相对于55.跳跃游戏还是难了不少。但思路是相似的，还是要看最大覆盖范围。

本题要计算最小步数，那么就要想清楚什么时候步数才一定要加一呢？

        贪心的思路，局部最优：当前可移动距离尽可能多走，如果还没到终点，步数再加一。整体最优：一步尽可能多走，从而达到最小步数。

        思路虽然是这样，但在写代码的时候还不能真的就能跳多远跳远，那样就不知道下一步最远能跳到哪里了。

        所以真正解题的时候，要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最小步数！

        这里需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖。

        如果移动下标达到了当前这一步的最大覆盖最远距离了，还没有到终点的话，那么就必须再走一步来增加覆盖范围，直到覆盖范围覆盖了终点。

如图：

         图中覆盖范围的意义在于，只要红色的区域，最多两步一定可以到！（不用管具体怎么跳，反正一定可以跳到）

方法1:贪心

        从图中可以看出来，就是移动下标达到了当前覆盖的最远距离下标时，步数就要加一，来增加覆盖距离。最后的步数就是最少步数。

这里还是有个特殊情况需要考虑，当移动下标达到了当前覆盖的最远距离下标时

• 如果当前覆盖最远距离下标不是是集合终点，步数就加一，还需要继续走。
• 如果当前覆盖最远距离下标就是是集合终点，步数不用加一，因为不能再往后走了。

Go代码如下：

func jump(nums []int) int {
    if len(nums) == 1 {
        return 0
    }
    ans := 0 //记录走的最大步数
    cur_distance := 0 //当前覆盖最远距离的下标
    next_distance := 0 //下一步的覆盖最远距离的下标
    for i:=0;i<len(nums);i++{
        next_distance = max(i+nums[i], next_distance)   //更新下一步覆盖最远距离下标
        if i == cur_distance { // 如果当前下标到了当前覆盖的最远距离的下标了，有如下两种情况
            if cur_distance != len(nums)-1 {    //1.如果当前覆盖最远距离下标不是终点  
                ans++   //需要继续走路咯
                cur_distance = next_distance //更新当前覆盖最远距离下标（相当于加油了）
                if next_distance >= len(nums)-1{    //下一步的覆盖范围已经可以达到终点
                    break
                }
            } else if cur_distance == len(nums)-1 {// 2.当前覆盖最远距离下标是集合终点，不用ans++了，直接结果返回
                break
            }
        }
    }
    return ans
}
func max(a, b int) int {
    if a > b {
        return a 
    }
    return b
}

第三题不是很懂，我们🐭🐭啊，就是这样的捏🤣