多元函数偏导数连续、存在与可微的关系

偏导数连续、可微、偏导数存在三者之间的关系

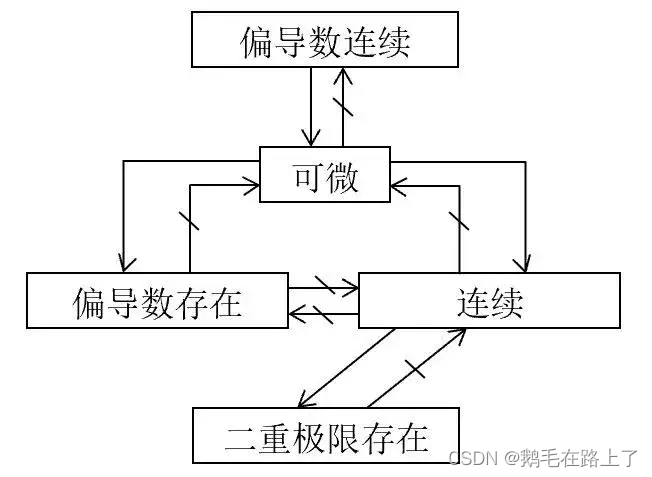
注意，以上关系图中均为单向箭头，即全是必要条件（若$p<=q(p\ne >q)$，则p是q的必要（不充分）条件，如p为矩阵A,B的秩相等，q为A~B（A相似于B），仅能有q推出p，而不能由p推出q，即p存在不一定能推q，但q存在一定能推出p）;

其中偏导数连续是最强条件，可以推可微，可以推偏导数存在，可以推连续（连续必然极限存在）;

概念回顾

多元函数求极限

除洛必达法则、单调有界准则不能照搬使用外，其他求极限的方法同一元函数求极限的一致。

多元函数求极限的具体例题、系统方法可参考：零蛋大——多元函数求极限方法总结

多元函数连续

即函数$f(x,y)在(x_0,y_0)$上的极限值等于$f(x_0,y_0)$

偏导数

可微

可微的充分条件（定义式）

可微的必要条件（偏导数存在）

若函数在某点(x,y)处的偏导数不存在，则一定不可微，即偏导数存在不一定能可微，但偏导数不存在一定不可微！

例题

2012 数学一真题：

选项A. 若$f(x,y)$就取分母$|x|+|y|$，显然满足极限存在，

但通过偏导数定义法求解$f(x,y)$的偏导数会出现一元函数中类似$\frac{|x|}{x}$含尖点的情况，

则偏导数是不存在的，故不能推出可微；

带绝对值的函数一般都是不可微的（一元中不可导），在多元函数积分学中这一点也会起到关键作用（当被积函数分母有绝对值，偏导数不存在时，不能利用高斯公式求解二型曲面积分，而只能用转换投影法）

选项C. 若$f(x,y)$在(0,0)处可微，可以取平面$f(x,y)=1$，显然$f(x,y)$在(0,0)处可微，但选项C的极限为“1/0趋于∞”，极限并不存在；

选项D. 同上；

选项B. 由选项B中的极限，可以推出$f(0,0)=0$（$f(x,y)$必为$无穷小量x^2+y^2趋于0$的高阶无穷小），

且可以通过偏导数定义法（公式法）求出$f_x^{\prime }(0,0)=f_y^{\prime }(0,0)=0$，再代入可微的定义式中，可以证明满足可微的充分条件，故B正确；

但从应试技巧上讲，这已经是当年高数选择题中最难的一道概念题了，不管掌握得是否全面，根据排除法已经能做对这道题了.