数据结构(C语言版)严蔚敏---＞常用的查找算法[静态查找表、动态查找表]

1. 静态查找表和动态查找表

首先，先明白查找表这个概念。
查找表：用来查找的数据集合称为查找表，它由同一类型的数据元素（或记录）组成，可以是一个数组或链表等数据类型。对查找表经常进行的操作一般有4种：

• 1.查找某个特定的数据元素是否在查找表中；
• 2.检索满足条件的某个特定的数据元素的各种属性；
• 3.在查找表中插入一个数据元素；
• 4.从查找表中删除某个特定的数据元素。

静态查找表：一个查找表的操作只涉及上述操作1和2，无须动态修改查找表，此类查找表称为静态查找表。
动态查找表：需要动态地插入或删除的查找表称为动态查找表。

适合静态查找表的查找方法有顺序查找、折半查找、散列查找。
适合动态查找表的查找方法有二叉排序树的查找、散列查找。

2. 顺序查找和折半查找

2.1 顺序查找

顺序查找又称线性查找，它对顺序表和链表都适用。
顺序查找是最简单的一种查找方法，基本思想为从线性表的一段开始，逐个检查关键字是否满足给个的条件。为了很多不必要的判断语句，通常在算法中引入“哨兵”。

int Search_Seq(SSTable S,ElemType key){
    S.elem[0] = key;
    // 哨兵
    int i;
    for(i=S.length;S.elem[i]!=key;--i);
    return i;
}
1
2
3
4
5
6
7

对于n个元素的表，给定值key与表中第i个元素相等，则定位到第i个元素时，需要比较i次(参考书上写n-i+1)关键字的比较。查找成功时，顺序查找的平均长度为

P1*1+P2*2+...+Pi*i（i从1到n）
或P1*(n-1+1)+P2*(n-2+1)+...+Pi*(n-i+1)（i从1到n）
其中Pi=1/n(i从1到n)
1
2
3

ASL成功 = (n+1)/2
时间复杂度为O(n)

2.2 折半查找

折半查找又称为二分查找，它适用于有序的顺序表。

int Binary_Search(SSTable S,ElemType key){
    int low = 0,high = S.length-1,mid;
    while(low<=high){
        mid = (low+high)/2;
        if(S.elem[mid] == key)
            return mid;
        else if(S.elem[mid] > key)
            high = mid - 1;
        else
            low = mid + 1;
    }
    return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

运行结果：

【注】：数组下标从0开始。
折半查找的执行过程为：

7 10 13 16 19 29 32 33 37 41 43
low = 0,high = 10
mid = 10/2 = 5 对应29 < 32,low = 5+1 = 6

32 33 37 41 43
low = 6,high = 10
mid = 16/2 = 8 对应37 > 32,high = 8-1 = 7

32 33 
low = 6,high = 7
mid = 13/2 = 6 对应32 = 32 返回6
1
2
3
4
5
6
7
8
9
10
11

折半查找的过程可以用下图所示的二叉树来描述(来自参考书)。

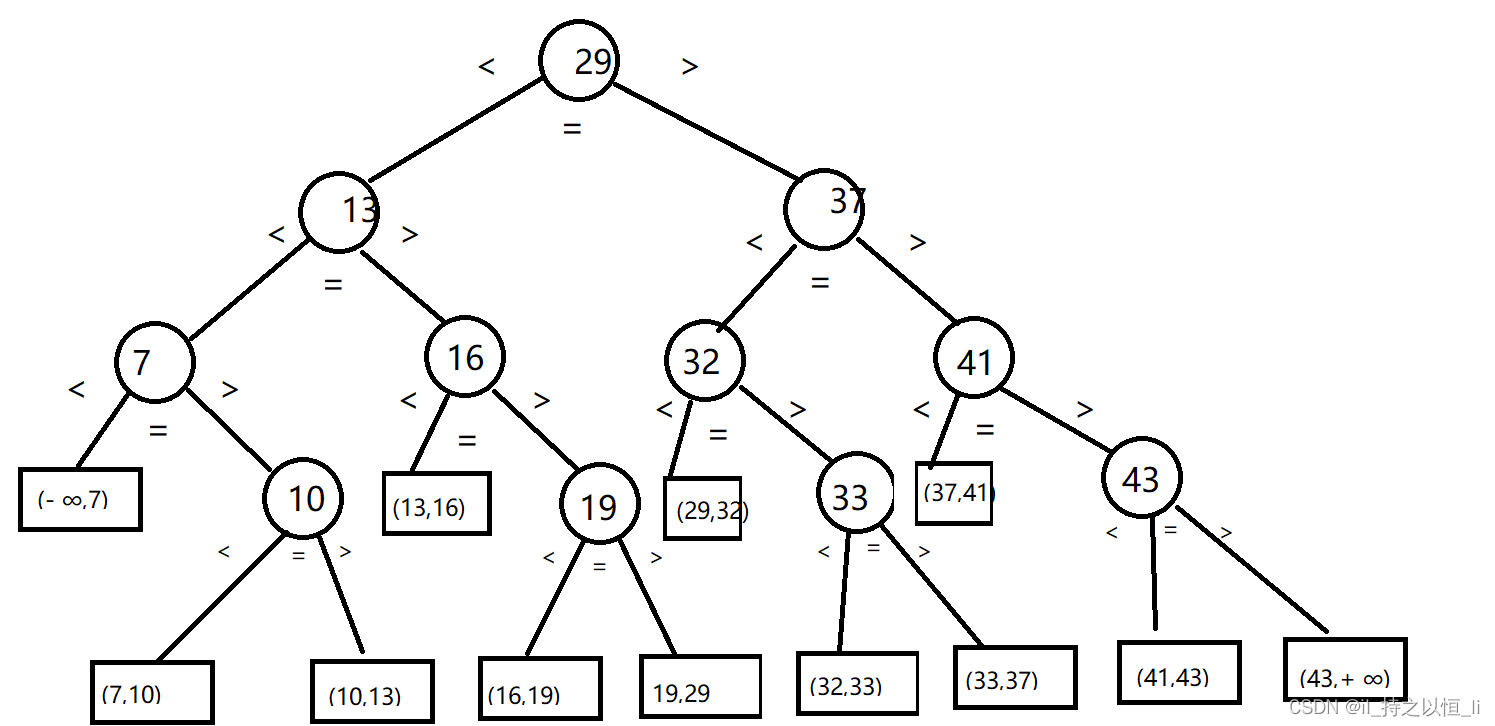
用折半查找法查找给定值的比较次数最多不会查过树的高度。其查找成功的平均查找长度为
ASL = (11+22+…+h*2^(h-1))/n = [(n+1)/n]*log 2 (n+1)
折半查找的时间复杂度为O(log 2 n)

3. 散列表

散列表是根据关键字而直接进行访问的数据结果。散列表建立了关键字和存储地址之间的一种直接映射关系。

3.1 散列函数

1. 直接定址法，直接去关键字的某个线性函数为散列地址，散列函数可以为H(key)=key或H(key)=key*a+b(a,b均为常数)，这种方法不会产生地址“冲突”，但是容易造成存储空间的浪费。它适合关键字分布基本连续的情况。
2. 除留余数法，最简单、最常用的方法，取一个不大于m（m为散列表长度）但接近或m的质数p，散列函数为H(key) =key%p。
3. 数字分析法，这种方法适合与已知的关键字集合.
4. 平方取中法，取关键字的平方值的中间几位作为散列地址，这种方法适用于关键字的每位取值都不够均匀或者均小于散列地址所需的位数。

3.2 处理冲突的方法

1.开放地址法，指可存放新表项的空闲地址既向它的同义词表项开放，也向它的非同义词开放。

数学递推公式为Hi=(H(key)+di)%m
H(key)为散列函数，m表示散列表的长度，di为递增序列。

取某一递增序列，对应的处理方法就是确定的。

• 线性探测法。di=0，1，2，3，…，m-1时，称为线性探测法。这种方法很容易造成同义词、非同义词的”聚积(堆积)现象“
• 平方探测法。

当di=0^2 ,1*2 ,(-1)^2 ,...,(-k)^2，称为平方探测法，
其中k<=m/2(m为散列表的长度,且m必须可以表示成4k+3的素数) 
1
2

又称二次探测法，可以避免”堆积“问题，缺点是不能探测散列表的所有单元，但至少可以探测到一半单元。

• 双散列法，di=Hash2(key)时，称为双散列法。需要使用两个散列函数，当通过第一个散列函数H(key)得到的地址发生冲突时，则利用第二个散列函数作为该关键字的增量。
  具体表达式为Hi=(H(key)+i*Hash2(key))%m，其中i是冲突次数，初始为0。在双散列法中，最多探测m-1次即可遍历表中所有位置，回到初始探测位置。
• 伪随机序列法。当di=伪随机序列时。

2 拉链法(链接法)
适用于经常进行插入和删除的情况。
对于不同的关键字可能通过散列函数映射到同一地址，为了避免非同义词产生冲突，可以把所有同义词存储在一个线性链表中，这个线性链表由其散列地址唯一标识。
如 关键字序列为 13 15 17 22 9 7 4，散列函数H(key)=key%7,用拉链法解决冲突可以得到如下