动态规划之空间压缩技巧

不管是哪个动态规划，如果依赖的只是相邻位置，那么就可以使用空间压缩方法。

• 情况一：(i,j) 位置依赖于 (i-1,j) 和 (i,j-1)，则从左往右 求 （题目"动态规划：路径最小累加和（经典）" 即使用的这种压缩技巧）
  

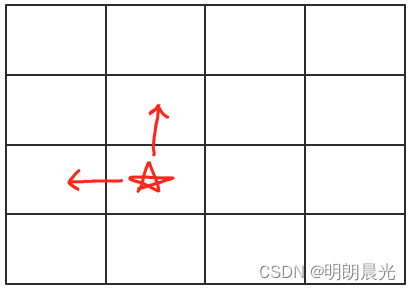
• 情况二：(i,j) 位置依赖于 (i-1,j-1) 和(i-1,j)，则从右往左 求
  如果某个动态规划中的某个位置依赖左上角的值和正上方的值，也能做数组压缩。
  
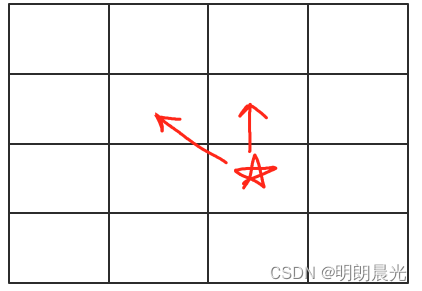
  这种情况的第0行都能由自身得到，因为第0行没有左上角和上方位置，类似于base case，其他位置就 从右往左 求，值没有更新的时候代表上一行的值，更新后代表这一行的值。

不管什么动态规划问题，只要满足这种依赖关系，都可以进行数组压缩。

• 情况三：(i,j) 位置依赖于(i-1,j-1)、(i-1,j) 和(i,j-1)，增加一个临时变量，并从左往右求
  
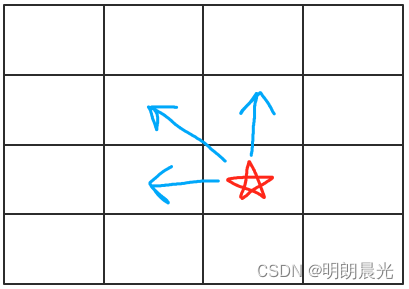
  第 0 行的值都能通过0行左边的值得到，因为第 0 行没有左上角和正上方。第 0 列的值通过第0列的上方的值得到，因为该列没有左边和左上角的值。

  假设第0行arr[a, b, c]，那么第1行的第0列的值a'可以通过a 得到，但是在将a' 填回该一维数组之前，用一个变量t记录下原始的a，此时一维数组中的值为[a',b,c]，而t = a，则b' 位置依赖的三个位置的值都已经得到了：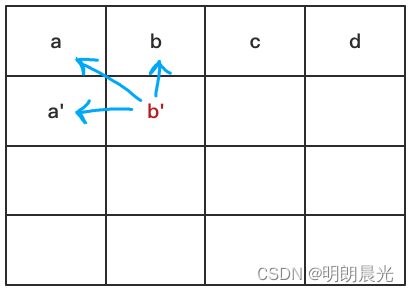

如果脑海中的 dp 表是 n（行） * m（列） 大小的，就需要准备一个 m 个元素空间的数组，这种情况下，如果 100w * 4，那只需要一个长度为 4 的数组即可，执行100w次，竖向更新，很好；但是如果是 4 * 100w 的矩阵呢？仍然只需要准备一个长度为 4 的数组，横向更新（如下图所示）。

这种推导方式和上文描述的一样，可以先得到第 0 列的值，通过第 0 列推导出第 1 列的值，然后按照依赖关系推导其他普遍位置，是完全可以的。

总结来说就是看如果行比较小，则一列一列地更新；如果列比较小，就一行一行地更新。