LCR 013. 二维区域和检索 - 矩阵不可变(java)

LCR 013. 二维区域和检索 - 矩阵不可变

题目

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 的子矩阵的元素总和。

 示例：

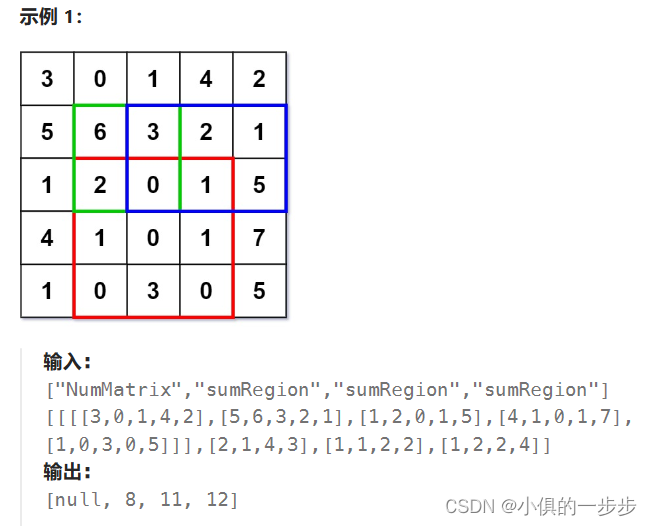
解题思路：

题目求子矩阵元素的和，首先想到的是暴力解法，两个for循环，将矩阵中的元素遍历相加，但是超出了时间限制。

将暴力求和优化：

思路：

 创建一个新的矩阵sums，每个元素表示该位置到已知矩阵[0, 0]，元素的和，为了减少边界的判断，直接创建比原来矩阵多一行一列的sums的矩阵：

图解：

求sums矩阵 

  this.sums[i][j] = this.sums[i-1][j]+this.sums[i][j-1]-this.sums[i-1][j-1]+matrix[i-1][j-1];

图解： 

 

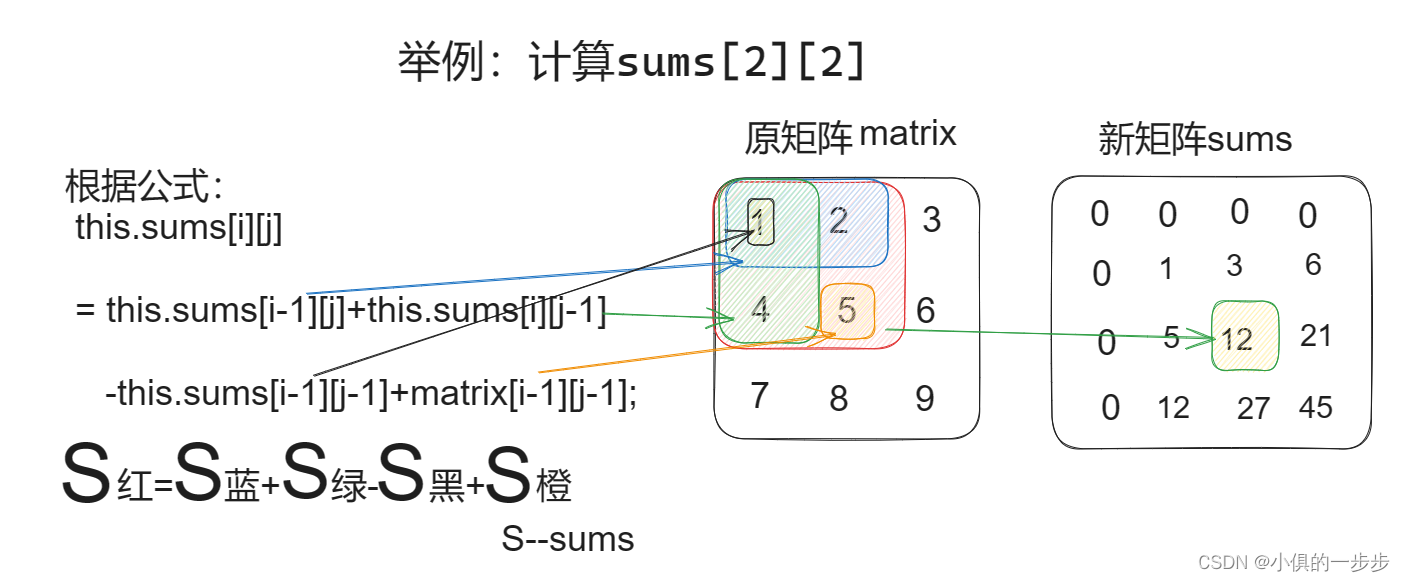
初始化 sums矩阵后，求子矩阵元素之和：

图解：

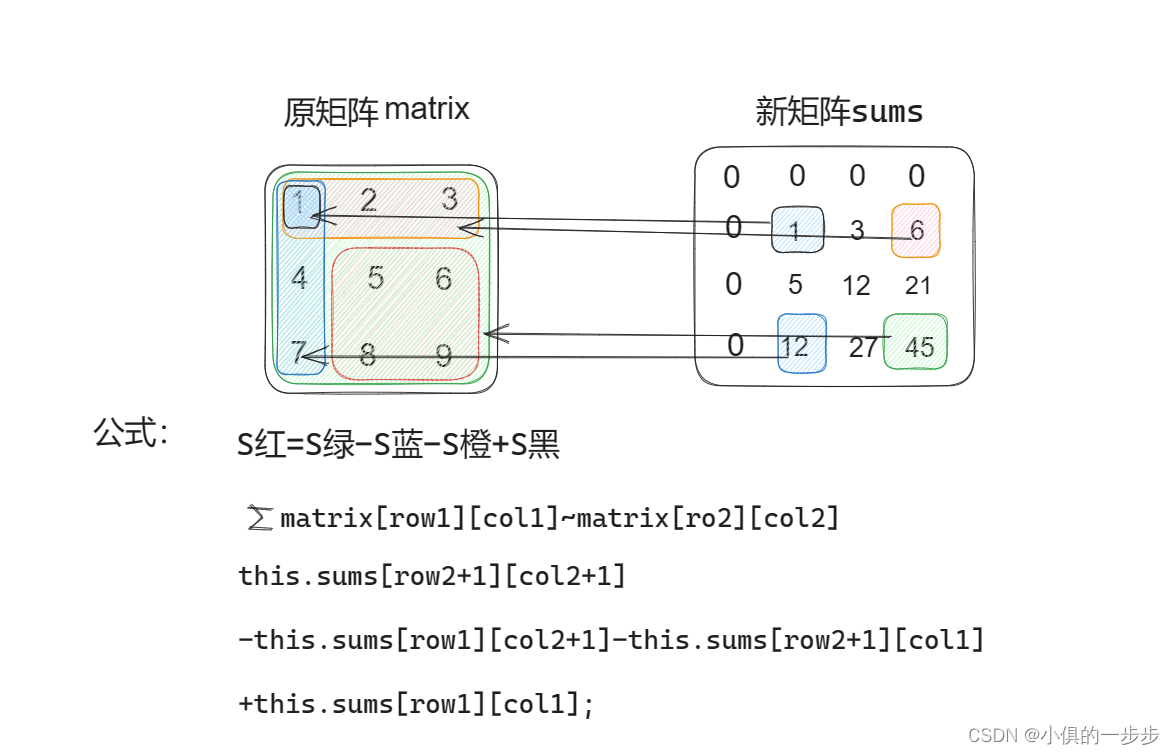
最终求解程序：

class NumMatrix {
 
    int[][] matrix;
 
    int[][] sums;
    public NumMatrix(int[][] matrix) {
       this.matrix = matrix;
        this.sums = new int[matrix.length+1][matrix[0].length+1];
        for (int i = 1; i <= matrix.length; i++) {
            for (int j = 1; j <= matrix[0].length; j++) {
               this.sums[i][j] = this.sums[i-1][j]+this.sums[i][j-1]-this.sums[i-1][j-1]+matrix[i-1][j-1];
            }
        }
    }
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return this.sums[row2+1][col2+1]-this.sums[row1][col2+1]-this.sums[row2+1][col1]+this.sums[row1][col1];
    }
}